AdaBoost, is short for adaptive boosting. Boosting can give good results even if the base classifiers have a performance that is only slightly better than random, and hence sometimes the base classifiers are known as weak learners. Originally designed for solving classification problems, boosting can also be extended to regression.
Adaboost算法流程
初始化每一个数据的权重系数
weighting coefficients{$w_n$}: $w_n^{(1)}$ = 1/N for n = 1,…,N.For m = 1,…,M:
- 在训练数据上训练 一个分类器
classifier$y_m(x)$ ,使得加权的错误率最低:
$$
J_m = \sum_{n=1}^Nw_n^{(m)}I(y_m( {\textbf x_n})\neq t_n)
$$
- 在训练数据上训练 一个分类器
其中$I(y_m({\textbf x_n})\neq t_n)$是指示函数,当$y_m({\textbf x_n})\neq t_n$时,这个函数为1,其余的时候为0.
计算下面的式子:
$$
\epsilon_{m}=\frac{\sum_{n=1}^{N}w_{n}^{(m)}I(y_{m}(\textbf x_n)\ne t_{n})}{\sum_{n=1}^{N}w_{n}^{(m)}}
$$
利用上面的式子去计算$\alpha_m$:
$$
\alpha_{m}=ln\{\frac{1-\epsilon_{m}}{\epsilon_{m}}\}
$$更新权重系数
$$
w_{n}^{(m+1)}=w_{n}^{(m)}exp[ \alpha_{m}I(y_{m}(\textbf x_n)\neq t_{n}) ]
$$
- 利用最后的模型做出预测:
$$
Y_M(\textbf {x}) = sign(\sum_{m=1}^M\alpha_my_m(\textbf x))
$$
理论解释—对指数误差函数的顺序最小化
指数误差函数:
$$
E=\sum_{n=1}^{N}exp[ -t_{n}f_{m}(\textbf x_n) ]
$$
其中$f_{m}(\textbf x)$可以看作是基础分类器$y_{l}(\textbf x)$的线性组合:
$$
f_{m}(\textbf x)=\frac{1}{2}\sum_{l=1}^{m}\alpha_{l}y_{l}(\textbf x)
$$
且$t_n\in\{ -1,1\}$是训练的目标值.我们的目标是根据权重系数$\alpha_{l}$ 以及$y_l(\textbf x)$ 来最小化指数误差函数E.
在这里我们假定基础的分类器$y_{1}(\textbf{x}), …, y_{m-1}(\textbf{x})$ 以及他们的系数$\alpha_{1}, …, \alpha_{m-1}$是固定的,我们不对误差函数做全局的最小化,而是仅仅针对$\alpha_{m}$ and $y_{m}(\textbf{x})$做最小化.
因此我们重写这个误差函数:
$$
E =\sum_{n=1}^{N}exp\{-t_{n}f_{m-1}(\textbf x_n)-\frac{1}{2}t_{n}\alpha_{m}y_{m}(\textbf x_n)\} \
=\sum_{n=1}^{N}w_{n}^{(m)}exp\{-\frac{1}{2}t_{n}\alpha_{m}y_{m}(\textbf x_n)\}
$$
其中在我们仅对$\alpha_{m}$ and $y_{m}(\textbf{x})$ 做最优化, 所以$w_{n}^{(m)}=exp\{-t_{n}f_{m-1}(\textbf x_n)\}$可以被认为是常数. 如果我们用$\Gamma_{m}$代表被 $y_{m}(\textbf{x})$ 分对的样本点, $\mathcal M_m$ 代表分错的样本点,那么我们可以把错误方差能写成如下的形式
$$
\begin{align}
E & = e^{-\alpha_{m}/2}\sum_{n\in \Gamma_{m}}w_{n}^{(m)}+e^{\alpha_{m}/2}\sum_{n\in \mathcal M_m}w_{n}^{(m)} \\
& = e^{-\alpha_m/2}\sum_{n\in \Gamma_{m}}w_{n}^{(m)}+e^{-\alpha_{m}/2}\sum_{n\in \mathcal M_m}w_{n}^{(m)}+(e^{\alpha_{m}/2}-e^{-\alpha_{m}/2})\sum_{n\in \mathcal M_m}w_{n}^{(m)} \\
& = e^{-\alpha_{m}/2}\sum_{n=1}^Nw_{n}^{(m)}+(e^{\alpha_{m}/2}-e^{-\alpha_{m}/2})\sum_{n=1}^Nw_{n}^{(m)}I(y_{m}(\textbf x_n)\neq t_{n})
\end{align}
$$
当我们对$y_{m}(\textbf{x})$求导的时候,第一项是常数,所以对错误方差求最小值就相当于在adaboost算法中最小化$J_m$ ,因为前面的系数不会影响最小值的位置.相似的,我们对$\alpha_{m}$求导,
$$
\frac{\partial E}{\partial \alpha_{m}} = -\frac{1}{2}e^{-\alpha_{m}/2}\sum_{n=1}^Nw_{n}^{(m)}+\frac{1}{2}(e^{\alpha_{m}/2}+e^{-\alpha_{m}/2})\sum_{n=1}^Nw_{n}^{(m)}I(y_{m}(\textbf x_n))\neq t_{n})=0
$$
$$
\epsilon_{m}=\frac{\sum_{n=1}^{N}w_{n}^{(m)}I(y_{m}(\textbf x_n)\neq t_{n})}{\sum_{n=1}^{N}w_{n}^{(m)}} = \frac{e^{-\alpha_{m}/2}}{e^{\alpha_{m}/2}+e^{-\alpha_{m}/2}}
$$
$$
\frac{1}{\epsilon_{m}}= \frac{e^{\alpha_{m}/2}+e^{-\alpha_{m}/2}}{e^{-\alpha_{m}/2}}=1+e^{\alpha_{m}}
$$
$$
\alpha_{m}=ln(\frac{1}{\epsilon_{m}}-1)=ln((1-\epsilon_{m})/\epsilon_{m})
$$
与adaboost算法中一致.
由于$w_{n}^{(m)}=exp\{-t_{n}f_{m-1}(\textbf x_n)\}$,所以
$$
w_{n}^{(m+1)}=w_{n}^{(m)}exp\{-\frac{1}{2}t_{n}\alpha_{m}y_{m}(\textbf x_n)\}
$$
由于
$$
t_{n}y_{m}(\textbf x_n) = 1 - 2I(y_{m}(\textbf x_n)\neq t_{n})
$$
所以
$$
\begin{align}
w_{n}^{(m+1)}&=w_{n}^{(m)}exp\{-\frac{1}{2}t_{n}\alpha_{m}y_{m}(\textbf x_n)\} \\
&= w_{n}^{(m)}exp\{-\frac{1}{2}\alpha_{m}(1 - 2I(y_{m}(\text x_n)\neq t_{n}) \\
&=w_{n}^{(m)}exp\{-\frac{1}{2}\alpha_{m}\}exp\{\alpha_{m}I(y_{m}(\textbf x_n)\neq t_{n})
\}
\end{align}
$$
因为$exp\{-\frac{1}{2}\alpha_{m}\}$与n无关,每次更新的时候都是个常数,所以可以删除.
$$
w_{n}^{(m+1)}=w_{n}^{(m)}exp\{\alpha_{m}I(y_{m}(\textbf x_n)\neq t_{n})\}
$$
根据$f_{m}(\textbf x)=\frac{1}{2}\sum_{l=1}^{m}\alpha_{l}y_{l}(\textbf x)$的符号,我们可以得到与adaboost一致的结果,系数$\frac{1}{2}$可以舍掉.
基础Adaboost算法实践
data $X \in \mathbb{R}^{n\times p}$ label $y\in\{-1, +1\}^{n}$
weak learner 是 decision stump.
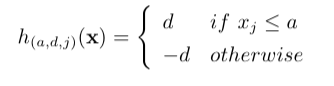
$a\in \mathbb{R}$, $j\in \{1, …, p\}$, $d\in \{-1, +1\}$. 其中 $\textbf{x}\in \mathbb{R}^{p}$ 是个向量,$x_{j}$ 是第$j$个元素.
数据地址:ada_data.mat
我们有1000个训练数据,每一个训练数据有25个特征,以及相应的一个label.
首先初始化weight,$\{\textbf x_i, y_i, w_i\}_{i=1}^n, w_i \geq 0,\sum_{i=1}^nw_i=1$
然后我们在 decision_stump.m 中返回decision stump的参数,这个参数是最小化加权的错误率$l(a^{\star}, d^{\star}, j^{\star})=min_{a, d, j}l(a, d, j)=min_{a, d, j}\sum_{i=1}^{n}w_{i}1\{h_{a, d, j}(\textbf x_i)\neq y_{i}\}$.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54function [k, a, d] = decision_stump(X, y, w)
% decision_stump returns a rule ...
% h(x) = d if x(k) ‚, ‚ otherwise,
%
% Input
% X : n * p matrix, each row a sample
% y : n * 1 vector, each row a label
% w : n * 1 vector, each row a weight
%
% Output
% k : the optimal dimension
% a : the optimal threshold
% d : the optimal d, 1 or -1
% total time complexity required to be O(p*n*logn) or less
%%% Your Code Here %%%
[m,n] = size(X);
minerror = inf;
minerror_a = 0;
minerror_j = -1;
minerror_d = 0;
w = w';
for i = 1:n
comp = repmat(X(:,i),1,m)';
ori_rep = repmat(X(:,i),1,m);
result_gt = double(ones(m,m));
result_gt((ori_rep - comp)>=0) = -1.0;
label_gt = repmat(y,1,m);
[min_value_gt,argmin_gt] = min(w*(result_gt ~= label_gt));
result_lt = double(ones(m,m));
result_lt((ori_rep - comp)<=0) = -1.0;
label_lt = repmat(y,1,m);
[min_value_lt,argmin_lt] = min(w*(result_lt ~= label_lt));
if min_value_lt < min_value_gt
final_error = min_value_lt;
final_a = X(argmin_lt,i);
final_d = -1.0;
else
final_error = min_value_gt;
final_a = X(argmin_gt,i);
final_d = 1.0;
end
if minerror > final_error
minerror = final_error
minerror_a = final_a;
minerror_d = final_d;
minerror_j = i;
end
end
k = minerror_j;
a = minerror_a;
d = minerror_d;
enddecision_stump_error.m update_weights.m adaboost_error.m adaboost.m
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26function w_update = update_weights(X, y, k, a, d, w, alpha)
% update_weights update the weights with the recent classifier
%
% Input
% X : n * p matrix, each row a sample
% y : n * 1 vector, each row a label
% k : selected dimension of features
% a : selected threshold for feature-k
% d : 1 or -1
% w : n * 1 vector, old weights
% alpha : weights of the classifiers
%
% Output
% w_update : n * 1 vector, the updated weights
%%% Your Code Here %%%
p = ((X(:, k) <= a) - 0.5) * 2 * d;
result = p;
w_update = w.*exp(alpha * (result ~= y));
%% 注意要normalization 保证公式分母是一样的
w_update = w_update/sum(w_update);
%%% Your code Here %%%
end